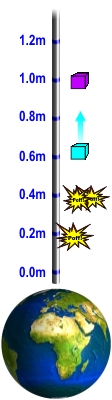
If we throw up an apple, or any other object, it will soon fall down again. Why - might one ask?
Isaac Newton would have said that there is a gravitational force acting on the object, pulling it down again. Albert Einstein in stead would say that the object returns because it's motion is described by a
For various reasons it is hard show directly what a curved spacetime really is - without a using any math. Here we will however use a trick that will allow us to visualize the curved spacetime with a curved surface.
Some properties of the full theory will be lost due to the trick, but many of the truly important features will remain. It will also give
The spacetime for a line outside the earth
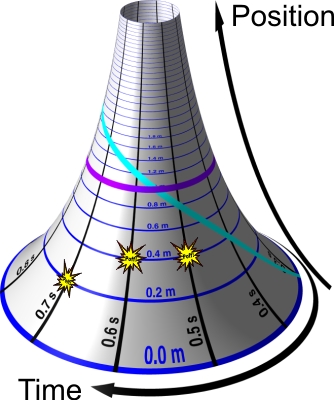
Consider an upright staff outside the earth. The spacetime of this staff can be illustrated by a curved surface as that depicted below. On the surface we can mark the events that happen on the staff. An event could for instance be somebody snapping his fingers at some position along the staff at a certain time. The higher the event occurs - the higher do we mark it on the surface. The later the event occurs - the more in the clockwise (as seen from above) direction around the surface do we mark it. We can also illustrate motion along the staff by a drawn curve on the spacetime. The faster the uppward motion the steeper the slope of the curve.


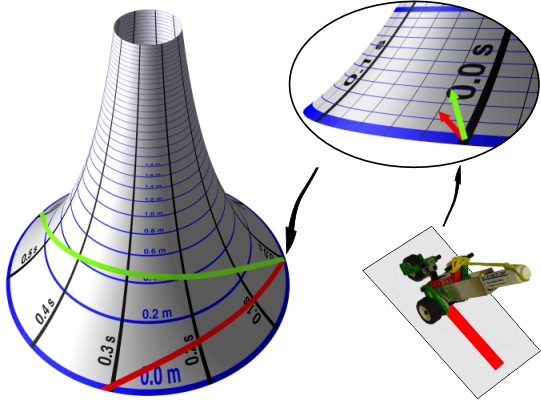
In Einsteins theory there is a law saying that a thrown-up object will have a motion corresponding to a straight line in the spacetime. Straight lines in the curved spacetime we can find using a little toy-car equipped with a pen. Just as it follows a straight line on a flat surface - so it does on a curved surface.
To predict the motion of an apple that we throw upwards, we start the drawing car at the base of the spactime - give it a direction corresponding to the throw-velocity of the apple - and let it roll forward along the surface to create a straight line. In the image below this process is repeated twice for different starting directions - corresponding to different throw-velocities.
Comments
Using the general technique underlying the illustration above we can explain much more about Einstein's theory of gravity. For the moment the above crash-course will however have to suffice:)